Hello ![]()
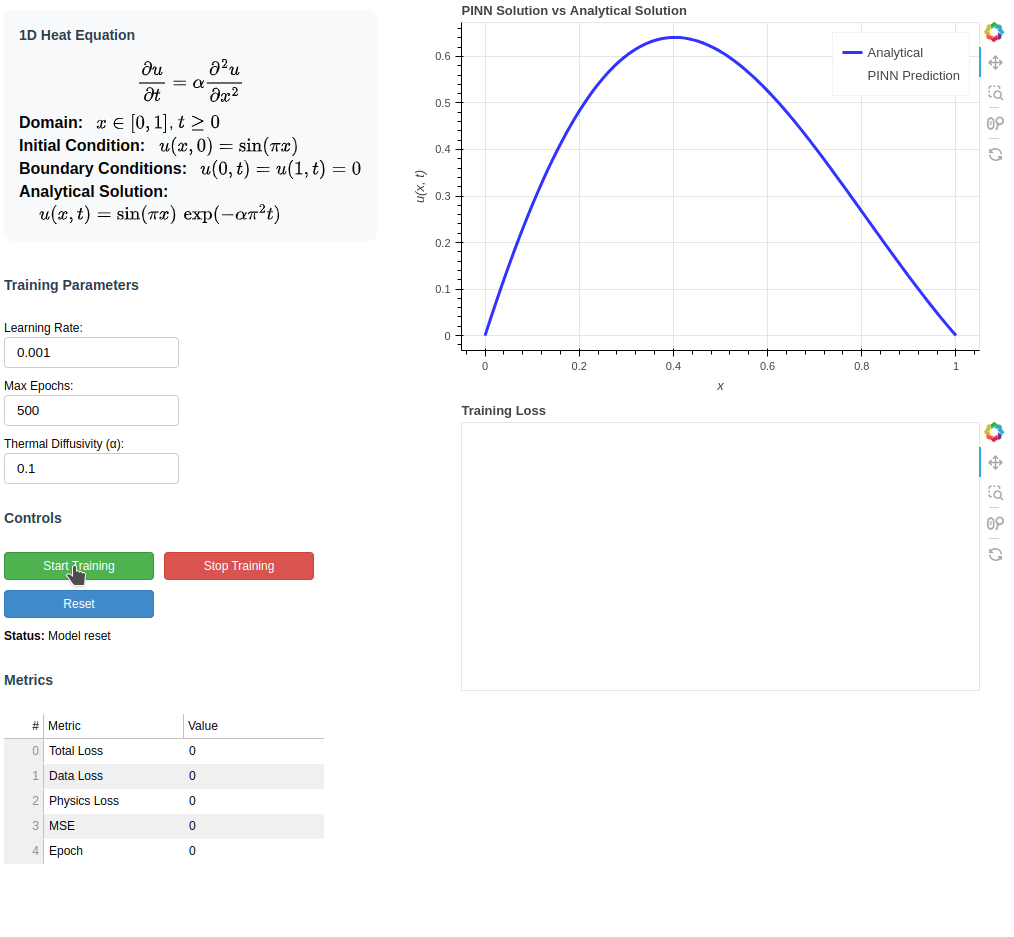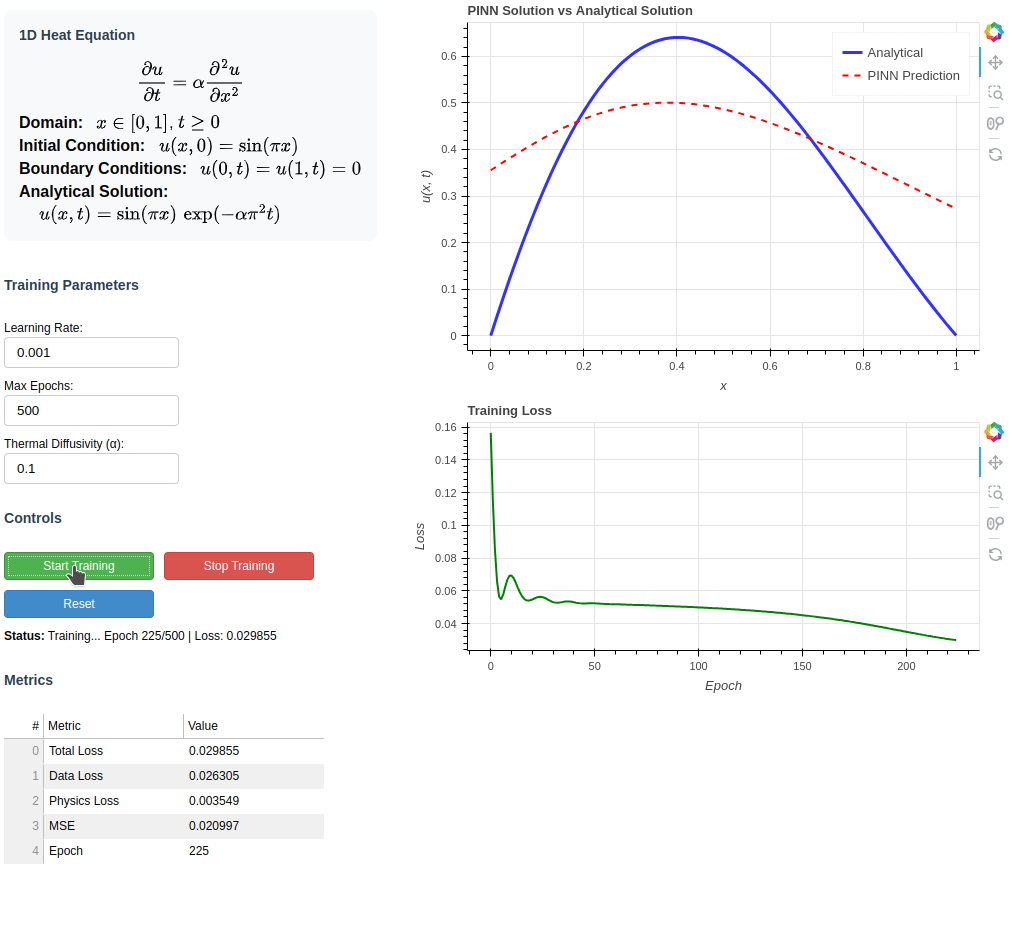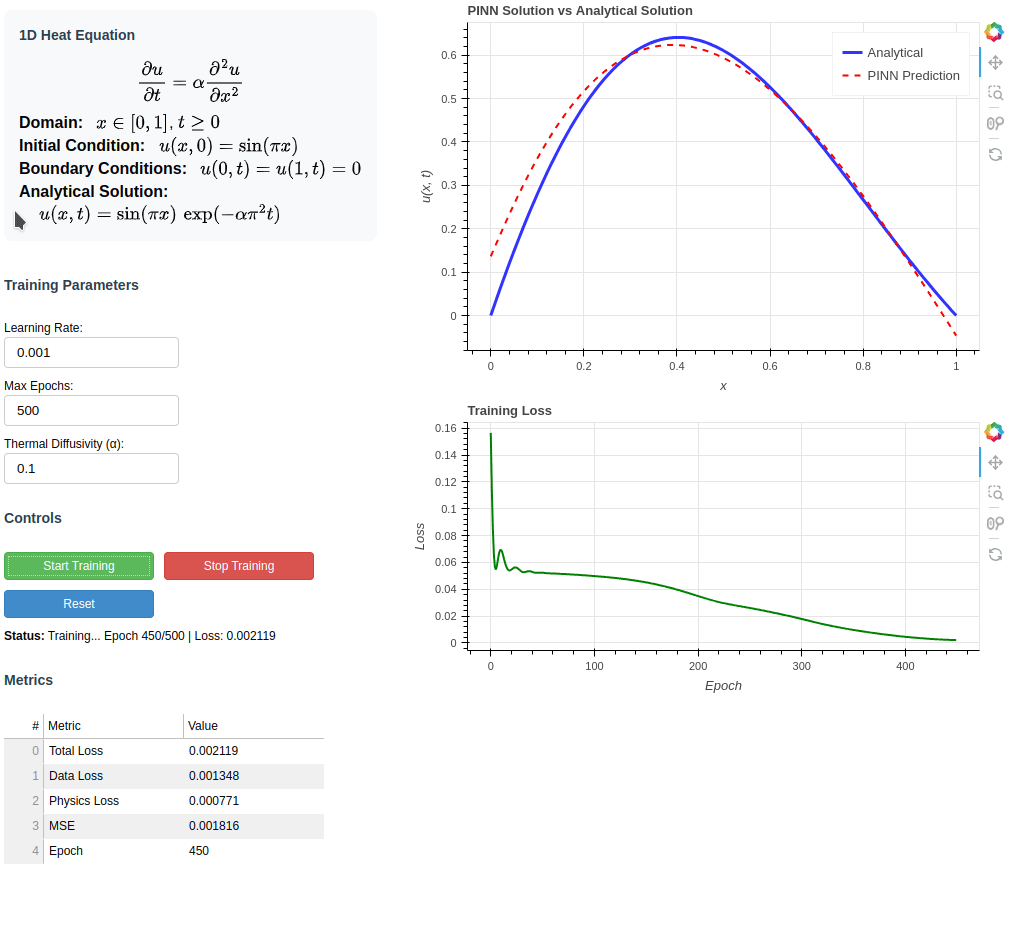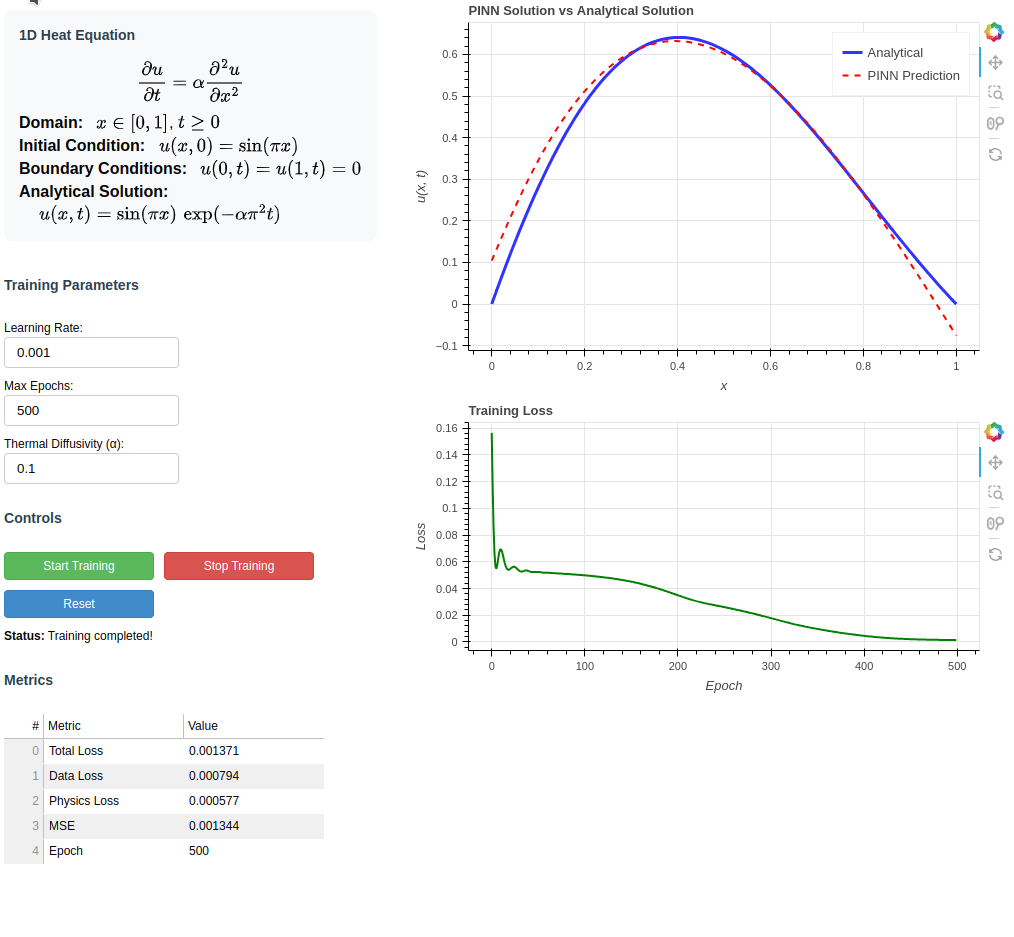
This interactive Bokeh application demonstrates a Physics-Informed Neural Network (PINN) for solving the 1D heat equation with Dirichlet boundary conditions.
Users can train the neural network directly in the browser, visualize both the analytical and neural network solutions, and adjust parameters such as the learning rate, number of epochs, and the thermal diffusivity α.
pip install bokeh torch numpy
# bokehPINN.py
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from bokeh.plotting import figure, curdoc
from bokeh.layouts import column, row
from bokeh.models import Button, TextInput, Div, DataTable, TableColumn, ColumnDataSource
import threading
import time
# --- PINN Model ---
class HeatEquationPINN(nn.Module):
def __init__(self, hidden=50):
super().__init__()
self.model = nn.Sequential(
nn.Linear(2, hidden),
nn.Tanh(),
nn.Linear(hidden, hidden),
nn.Tanh(),
nn.Linear(hidden, 1)
)
def forward(self, x, t):
xt = torch.cat([x, t], dim=1)
return self.model(xt)
def physics_loss(model, x, t, alpha):
x = x.clone().detach().requires_grad_(True)
t = t.clone().detach().requires_grad_(True)
u = model(x, t)
u_x = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u), create_graph=True)[0]
u_xx = torch.autograd.grad(u_x, x, grad_outputs=torch.ones_like(u_x), create_graph=True)[0]
u_t = torch.autograd.grad(u, t, grad_outputs=torch.ones_like(u), create_graph=True)[0]
residual = u_t - alpha * u_xx
return torch.mean(residual ** 2)
def generate_heat_eqn_data(num_samples=1000, alpha=0.1):
x = np.random.uniform(0, 1, (num_samples, 1)).astype(np.float32)
t = np.random.uniform(0, 1, (num_samples, 1)).astype(np.float32)
u = np.sin(np.pi * x) * np.exp(-alpha * (np.pi**2) * t)
return (torch.tensor(x), torch.tensor(t), torch.tensor(u))
def generate_test_data(n_points=100, alpha=0.1):
x = np.linspace(0, 1, n_points).reshape(-1, 1).astype(np.float32)
t = np.linspace(0, 1, n_points).reshape(-1, 1).astype(np.float32)
u = np.sin(np.pi * x) * np.exp(-alpha * (np.pi**2) * t)
return (torch.tensor(x), torch.tensor(t), torch.tensor(u))
# --- Bokeh App PINN Solver ---
class HeatEquationSolver:
def __init__(self):
self.model = None
self.optimizer = None
self.training = False
self.epoch = 0
self.losses = []
self.lr = 0.001
self.alpha = 0.1
self.max_epochs = 2000
self.batch_size = 1000
self.x_train, self.t_train, self.u_train = generate_heat_eqn_data(num_samples=self.batch_size, alpha=self.alpha)
self.x_test, self.t_test, self.u_test = generate_test_data(n_points=100, alpha=self.alpha)
self.x_train.requires_grad_()
self.t_train.requires_grad_()
self.x_test.requires_grad_()
self.t_test.requires_grad_()
def setup_data(self):
self.x_train, self.t_train, self.u_train = generate_heat_eqn_data(num_samples=self.batch_size, alpha=self.alpha)
self.x_test, self.t_test, self.u_test = generate_test_data(n_points=100, alpha=self.alpha)
self.x_train.requires_grad_()
self.t_train.requires_grad_()
self.x_test.requires_grad_()
self.t_test.requires_grad_()
def setup_model(self):
self.model = HeatEquationPINN(hidden=50)
self.optimizer = optim.Adam(self.model.parameters(), lr=self.lr)
self.losses = []
self.epoch = 0
def train_step(self):
self.model.train()
self.optimizer.zero_grad()
u_pred = self.model(self.x_train, self.t_train)
data_loss = torch.mean((u_pred - self.u_train) ** 2)
p_loss = physics_loss(self.model, self.x_train, self.t_train, self.alpha)
total_loss = data_loss + p_loss
total_loss.backward()
self.optimizer.step()
self.losses.append(total_loss.item())
self.epoch += 1
return total_loss.item(), data_loss.item(), p_loss.item()
def get_prediction(self):
if self.model is None:
# Before training, just show zeros or the ground truth
return np.zeros_like(self.u_test.cpu().numpy().flatten()), self.u_test.cpu().numpy().flatten()
self.model.eval()
with torch.no_grad():
pred = self.model(self.x_test, self.t_test)
return pred.cpu().numpy().flatten(), self.u_test.cpu().numpy().flatten()
# --- Bokeh Setup ---
doc = curdoc()
doc.title = "1D Heat Equation PINN Solver (PyTorch)"
solver = HeatEquationSolver()
# Data sources for Bokeh plots
source_true = ColumnDataSource(data=dict(x=[], y=[]))
source_pred = ColumnDataSource(data=dict(x=[], y=[]))
source_loss = ColumnDataSource(data=dict(epoch=[], loss=[]))
source_metrics = ColumnDataSource(data=dict(
metric=['Total Loss', 'Data Loss', 'Physics Loss', 'MSE', 'Epoch'],
value=[0.0, 0.0, 0.0, 0.0, 0]
))
plot_solution = figure(
title="PINN Solution vs Analytical Solution",
x_axis_label="x",
y_axis_label="u(x, t)",
width=600,
height=400,
tools="pan,wheel_zoom,box_zoom,reset"
)
plot_solution.line('x', 'y', source=source_true, legend_label="Analytical", line_width=3, color='blue', alpha=0.8)
plot_solution.line('x', 'y', source=source_pred, legend_label="PINN Prediction", line_width=2, color='red', line_dash='dashed')
plot_solution.legend.location = "top_right"
plot_loss = figure(
title="Training Loss",
x_axis_label="Epoch",
y_axis_label="Loss",
width=600,
height=300,
tools="pan,wheel_zoom,box_zoom,reset"
)
plot_loss.line('epoch', 'loss', source=source_loss, line_width=2, color='green')
# Controls
learning_rate_input = TextInput(value="0.001", title="Learning Rate:")
epochs_input = TextInput(value="2000", title="Max Epochs:")
alpha_input = TextInput(value="0.1", title="Thermal Diffusivity (α):")
start_button = Button(label="Start Training", button_type="success", width=150)
stop_button = Button(label="Stop Training", button_type="danger", width=150)
reset_button = Button(label="Reset", button_type="primary", width=150)
columns = [
TableColumn(field="metric", title="Metric"),
TableColumn(field="value", title="Value")
]
metrics_table = DataTable(source=source_metrics, columns=columns, width=320, height=200)
equation_div = Div(text=r"""
<div style="background: #f8f9fa; padding: 15px; border-radius: 8px; margin: 10px 0;">
<h3 style="color: #2c3e50; margin-top: 0;">1D Heat Equation</h3>
<div style="font-size: 16px; text-align: center; margin-bottom: 10px;">
$$
\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2}
$$
</div>
<div style="font-size: 16px; text-align: left;">
<b>Domain:</b> \(x \in [0, 1]\), \(t \geq 0\)<br>
<b>Initial Condition:</b> \(u(x, 0) = \sin(\pi x)\)<br>
<b>Boundary Conditions:</b> \(u(0, t) = u(1, t) = 0\)<br>
<b>Analytical Solution:</b><br>
  \(u(x, t) = \sin(\pi x)\, \exp(-\alpha \pi^2 t)\)
</div>
</div>
<script>
if (typeof MathJax !== 'undefined') { MathJax.typesetPromise(); }
</script>
""", width=400)
status_div = Div(text="<b>Status:</b> Ready to train", width=350)
def update_plots():
# For t_test=linspace(0,1), use the *first* t=0 for demo
x_plot = solver.x_test.detach().cpu().numpy().flatten()
y_true = solver.u_test.detach().cpu().numpy().flatten()
y_pred, _ = solver.get_prediction()
source_true.data = dict(x=x_plot, y=y_true)
source_pred.data = dict(x=x_plot, y=y_pred)
epochs = list(range(len(solver.losses)))
source_loss.data = dict(epoch=epochs, loss=solver.losses)
def update_metrics(total_loss, data_loss, p_loss):
y_pred, y_true = solver.get_prediction()
mse = np.mean((y_true - y_pred)**2)
source_metrics.data = dict(
metric=['Total Loss', 'Data Loss', 'Physics Loss', 'MSE', 'Epoch'],
value=[
f"{total_loss:.6f}", f"{data_loss:.6f}", f"{p_loss:.6f}",
f"{mse:.6f}", solver.epoch
]
)
def training_loop():
while solver.training and solver.epoch < solver.max_epochs:
total_loss, data_loss, p_loss = solver.train_step()
if solver.epoch % 25 == 0:
doc.add_next_tick_callback(update_plots)
doc.add_next_tick_callback(lambda tl=total_loss, dl=data_loss, pl=p_loss:
update_metrics(tl, dl, pl))
doc.add_next_tick_callback(lambda: update_status(
f"Training... Epoch {solver.epoch}/{solver.max_epochs} | Loss: {total_loss:.6f}"
))
time.sleep(0.001)
if solver.training:
solver.training = False
doc.add_next_tick_callback(lambda: update_status("Training completed!"))
doc.add_next_tick_callback(update_plots)
def update_status(message):
status_div.text = f"<b>Status:</b> {message}"
def start_training():
if solver.training:
return
try:
solver.lr = float(learning_rate_input.value)
solver.max_epochs = int(epochs_input.value)
solver.alpha = float(alpha_input.value)
solver.setup_data()
solver.setup_model()
solver.training = True
update_status("Training started...")
training_thread = threading.Thread(target=training_loop)
training_thread.daemon = True
training_thread.start()
except Exception as e:
update_status(f"Error: {e}")
def stop_training():
solver.training = False
update_status("Training stopped")
def reset_model():
solver.training = False
solver.epoch = 0
solver.losses = []
solver.model = None
source_pred.data = dict(x=[], y=[])
source_loss.data = dict(epoch=[], loss=[])
source_metrics.data = dict(
metric=['Total Loss', 'Data Loss', 'Physics Loss', 'MSE', 'Epoch'],
value=[0.0, 0.0, 0.0, 0.0, 0]
)
update_status("Model reset")
# Attach callbacks
start_button.on_click(start_training)
stop_button.on_click(stop_training)
reset_button.on_click(reset_model)
update_plots()
controls = column(
equation_div,
Div(text="<h3 style='color: #2c3e50;'>Training Parameters</h3>", width=300),
learning_rate_input,
epochs_input,
alpha_input,
Div(text="<h3 style='color: #2c3e50;'>Controls</h3>", width=300),
row(start_button, stop_button),
reset_button,
status_div,
Div(text="<h3 style='color: #2c3e50;'>Metrics</h3>", width=300),
metrics_table
)
main_content = column(plot_solution, plot_loss)
layout = row(controls, main_content)
doc.add_root(layout)
bokeh serve bokehPINN.py --show