Creating a linear regression animation in Bokeh

Community Support
1

Working through some online computer science exercises, I’ve really enjoyed learning Python and Bokeh together, however, I’ve struggled now for a number of weeks to understand Bokeh callbacks. The below code represents a simple linear regression algorithm.

matrix = [
	[1.2, 1.2],
	[3, 2.5],
	[5.1, 6],
	[6.3, 4.5],
	[7.1, 5.2],
	[8.2, 8.9],
	[9, 13.8],
	[11.2, 12.1],
	[13.8, 14.2],
]
matrix = list(zip(*matrix))
training = {"x": matrix[0], "y":matrix[1]}

learning_rate = 0.0001

def update(m, b):
	# Run through all training data and update and m and b for each
	final_m = m
	final_b = b
	for i in range(len(training["x"])):
		error = calculateError(training["x"][i], training["y"][i], final_m, final_b)
		deltaM = training["x"][i] * error * learning_rate
		deltaB = error * learning_rate
		final_m += deltaM
		final_b += deltaB
	return final_m, final_b

slopeData = ColumnDataSource(data = { "gradient":[0], "y_intercept":[0] })

def callback(m, b):
	new_data = dict()
	new_data["gradient"] = m
	new_data["y_intercept"] = b
	slopeData.data = new_data

def model():
	maxIterations = 1000
	iterations = 0
	model_m = 0.01
	model_b = 0.01
	parameterRecord = []
	lossRecord = []
	
	p = figure(width=800, height=800,title="Fitted Data",tools="",x_range=(0,15), y_range=(0,15))
	p.xaxis.axis_label = "x"
	p.yaxis.axis_label = "y"
	p.yaxis[0].ticker.desired_num_ticks = 30
	p.xaxis[0].ticker.desired_num_ticks = 30
	p.circle(x="x", y="y", source=training, size=12, color="red", alpha=.5)
	
	if iterations == 0:
		initalPoints = (model_m, model_b)
	else:
		pass
	initalSlope = Slope(gradient=initalPoints[0], y_intercept=initalPoints[1], line_width=3, line_alpha=0.2, line_color="blue")
	p.add_layout(initalSlope)


	while iterations < maxIterations:
		updatedSet = update(model_m, model_b)
		parameterRecord.append(updatedSet)
		p.add_layout(Slope(gradient="gradient", y_intercept="y_intercept", source=slopeData,\
			 line_width=2, line_alpha=0.3, line_color="red", callback=callback(model_m,model_b)))
		model_m, model_b = updatedSet
		iterations += 1

	finalPoints = parameterRecord[-1]
	finalSlope = Slope(gradient=finalPoints[0], y_intercept=finalPoints[1], line_width=4, line_alpha=0.6, line_color="red")
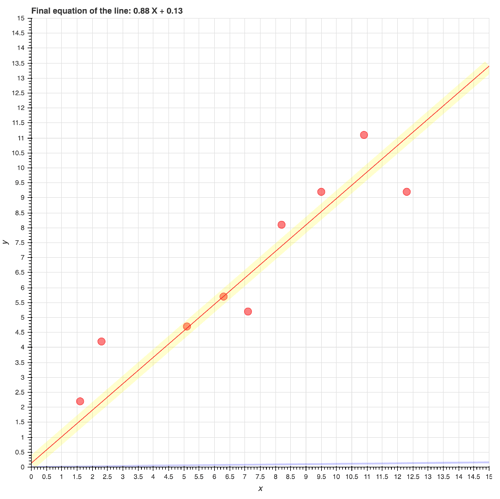
	print("Final equation of the line: {0:.2f} X + {1:.2f}".format(finalPoints[0],finalPoints[1]))
	p.add_layout(finalSlope)

	curdoc().add_root(p)

model()

…Which ends with the error:

ValueError: expected an element of ColumnData(String, Seq(Any)), got {'gradient': 0.01, 'y_intercept': 0.01}

Are there any suggestions on how to get this code to smoothly have the slope zoom in on the slope representing the minimized error? I’ve made some of the static examples on the main bokeh site into little animations, and feel like I’m really close on this example, but just can’t figure out the last couple of steps. I apologize if there are more basic errors in my Python code but at this point I know I really need to raise my hand and ask for help.

2

The proximate cause of that error is that the things you are storing in your ColumnDataSource are not columns (e.g. Python lists, Numpy arrays, or Pandas Series). You are initializing the data source correctly:

slopeData = ColumnDataSource(data={ "gradient": [0], "y_intercept": [0]} )

You can see there that all the values in the data dict are lists (columns). However at some point, you are trying to set values that are just plain numbers, and not columns. The message is telling you exactly what the bad values are:

{‘gradient’: 0.01, ‘y_intercept’: 0.01}

Those, as you can see, are not lists (or arrays). Presumably an immediately thing to try is to just put those values in Python lists inside the data dict:

new_data = dict()
new_data["gradient"] = [m]
new_data["y_intercept"] = [b]

However, I think you will have further issues. It’s not clear what you mean to accomplish by setting a callback on the Slope object. In fact, I am very surprised that is even allowed… Bokeh callbacks are usually attached to things the generate events, e.g. to sliders or buttons, or selections on data. You can also define periodic callbacks that simply execute on a prescribed regular interval.

3

Sometimes it seems like dictionaries, dataframes and CDS are interchangeable, and other times it needs to be quite exact. I appreciate the guidance and am working your suggestions into the code.

I noticed this too when I was working through the simpler animations that were modifications of other examples and then coming up against this problem. Periodic callbacks worked and I got other example’s elements to update every time I updated the CDS. However, other annotative elements don’t seem to work that way. Perhaps the easier solution is just to use line elements instead of slopes?

4

A CDS has a .data attribute which is always a dictionary that maps string names to sequences of values (“columns”). A Pandas DataFrame looks fairly similar to that description (a “mapping of names to columns”), so there are various places in the API that you can pass a DataFrame and it will “do the right thing”, as a convenience.

Periodic callbacks worked and I got other example’s elements to update every time I updated the CDS. However, other annotative elements don’t seem to work that way. Perhaps the easier solution is just to use line elements instead of slopes?

It’s not really possible to speculate without seeing actual code.

5 
def callback(m, b):
	x0 = 0
	x1 = 15
	y0 = (m * x0) + b
	y1 = (m * x1) + b
	return dict({"x": [x0,x1], "y":[y0,y1]})

line = p.line(x=[], y=[], line_width=20, alpha=0.2, line_color="yellow")
ds = line.data_source

while iterations < maxIterations:
	updatedSet = update(model_m, model_b)
	parameterRecord.append(updatedSet)
	line_dict = callback(model_m, model_b)
	new_data = dict()
	new_data["x"] = line_dict["x"]
	new_data["y"] = line_dict["y"]
	print(new_data)
	ds.data = new_data
	model_m, model_b = updatedSet
	iterations += 1

upload
upload1616×1614 251 KB

OK. Progress was made. It’s still not animating but I think I just need to hone in on the parameters or maybe add a delay to the loop.

6

There’s typically no point to ever having a loop like that updating state in a Bokeh server app. The reason being that the app script is only run once per session, to create the document for that session, before it is displayed. So your script makes a bunch of updates that are never displayed then whatever state is at the end is what is displayed, when the document it sent to the browser. To animate, you will most commonly want to use add_periodic_callback to run code after the session is loaded in the browser.

7

Yes. It’s starting to make sense now as I reverse engineered the weird behaviour of the last code update. What I might actually be looking for is:

curdoc().add_next_tick_callback

However, there doesn’t appear to be much documentation about how to use it. I suspect I can work it into the loop somehow but I might need to rework the project to work directly off a CDS. (And find a tutorial to about the thread module. :slight_smile: )

8

add_next_tick_callback is typically only useful when updating things from threads, though that would be another possible approach. There is an example in the *Running a Bokeh Server` chapter of the User’s Guide.