ScaleBar is not accurate when using geographical data

ernhollam · December 17, 2024, 10:33am

Hi Team,

Bokeh Info

Python version        :  3.12.8 | packaged by Anaconda, Inc. | (main, Dec 11 2024, 16:48:34) [MSC v.1929 64 bit (AMD64)]
IPython version       :  8.27.0
Tornado version       :  6.4.2
NumPy version         :  1.26.4
Bokeh version         :  3.6.0
BokehJS static path   :  C:\ProgramData\anaconda3\envs\BOKEH\Lib\site-packages\bokeh\server\static
node.js version       :  (not installed)
npm version           :  (not installed)
jupyter_bokeh version :  4.0.5
Operating system      :  Windows-11-10.0.26100-SP0

I am trying to use the ScaleBar annotation in a figure with geographical data.

When measuring distances according to the scale, I found out that the latter is not accurate.

Here is I hope a minimal enough code to reproduce the problem, I am using a Jupyter notebook in VS Code version 1.96.0:

import panel as pn
pn.extension(sizing_mode='scale_both')

from bokeh.plotting import figure
from bokeh.models import ScaleBar

from bokeh.io import output_notebook, curdoc
curdoc().clear()
output_notebook()

from bokeh.models import WMTSTileSource
from holoviews.util.transform import lon_lat_to_easting_northing
from geopy.distance import geodesic
from math import sin, cos, sqrt, atan2, radians

from bokeh.util.info import print_info
print_info()


rue_copernic_28 = (2.2885813, 48.869313)
rue_copernic_32 = (2.288077, 48.869387)

def create_figure():
    # définition des deux points (wgs84 vers PseudoMercator)
    x_rue_copernic_28, y_rue_copernic_28 = lon_lat_to_easting_northing(*rue_copernic_28)
    x_rue_copernic_32, y_rue_copernic_32 = lon_lat_to_easting_northing(*rue_copernic_32)

    # création de la figure avec les coordoonées en mercator
    fig = figure(x_axis_type='mercator', y_axis_type='mercator',
                 tools=['pan', 'box_zoom', 'wheel_zoom', 'save', 'reset'],
                 active_drag='pan', active_scroll='wheel_zoom',
                 title="Test échelles")
    # utilisation du serveur en ligne de images tuilées
    tiles = WMTSTileSource(url="https://data.geopf.fr/tms/1.0.0/GEOGRAPHICALGRIDSYSTEMS.PLANIGNV2/{Z}/{X}/{Y}.png",
                            name='PLAN IGN',
                            attribution="""
    <a href="https://geoservices.ign.fr/services-web-decouverte" target="_blank">&copy; Institut national de l'information géographique et forestière
    </a>""",
                            max_zoom=19)
    # ajout du fond de carte sur la figure
    fig.add_tile(tiles)
    
    # point 1
    fig.scatter(x_rue_copernic_28, y_rue_copernic_28, size=18, color='red', marker='circle_cross', line_color='black', legend_label='28 Rue Copernic')
    # point 2
    fig.scatter(x_rue_copernic_32, y_rue_copernic_32, size=18, color='green', marker='circle_cross', line_color='black', legend_label='32 Rue Copernic')
    
       
    # ajouter l'échelle seulement après avoir défini les limites
    fig.add_layout(ScaleBar())
    
    # mettre les légendes en bas à droite
    fig.legend.location = 'bottom_right'
    
    return fig

def calculer_distance_en_m(echelle_m, echelle_cm, mesure_cm):
    return echelle_m * mesure_cm/echelle_cm

def haversine_distance(point1, point2):
    # source : https://andrew.hedges.name/experiments/haversine/
    # Approximate radius of earth in m
    R = 6373.0*1e3

    lat1 = radians(point1[1])
    lon1 = radians(point1[0])
    lat2 = radians(point2[1])
    lon2 = radians(point2[0])

    dlon = lon2 - lon1
    dlat = lat2 - lat1

    a = sin(dlat / 2)**2 + cos(lat1) * cos(lat2) * sin(dlon / 2)**2
    c = 2 * atan2(sqrt(a), sqrt(1 - a))

    return R * c


map_pane = pn.pane.Bokeh(create_figure())
echelle = pn.widgets.FloatInput(name='Value échelle (m)', value=15)
mesure = pn.widgets.FloatInput(name='Mesure échelle (cm)', value=3.6)
mesure_entre_deux_points = pn.widgets.FloatInput(name='Mesure (cm)', value=14.7)
bokeh_distance = pn.widgets.FloatInput(name='Distance selon échelle (m)', disabled=True, value=pn.bind(calculer_distance_en_m, echelle, mesure, mesure_entre_deux_points))
geopy_distance = pn.widgets.FloatInput(name='Distance calculée avec Geopy (m)', disabled=True, value=geodesic((rue_copernic_28[1], rue_copernic_28[0]), (rue_copernic_32[1],rue_copernic_32[0])).km*1e3)
haversine_distance = pn.widgets.FloatInput(name='Distance haversine (m)', disabled=True, value=haversine_distance(rue_copernic_28, rue_copernic_32))

layout = pn.Row(map_pane, pn.WidgetBox("### Mesures", echelle, mesure, mesure_entre_deux_points, bokeh_distance, geopy_distance, haversine_distance))
layout

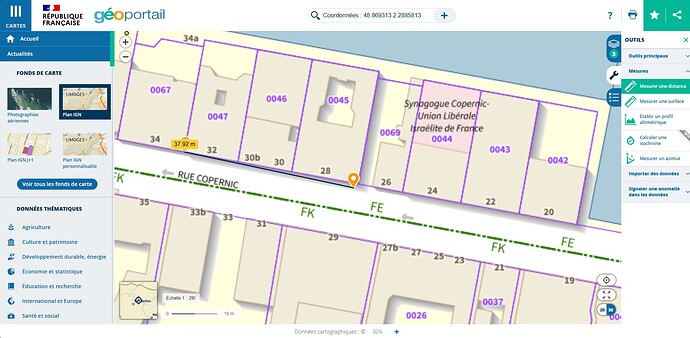
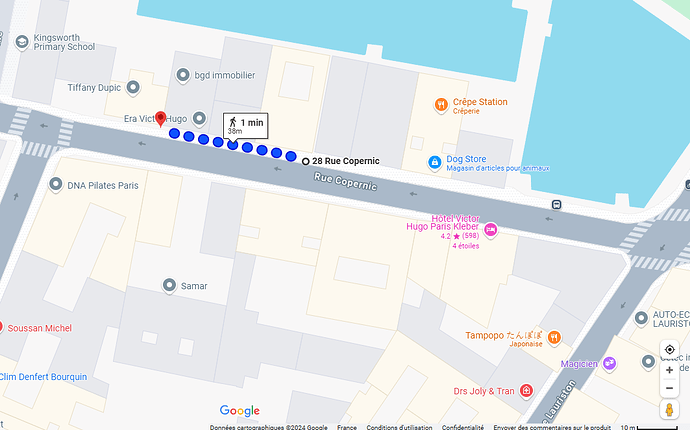
I compared with Geoportail (a French government site where we can analyse or visualize geographical data), Google Maps, Geopy’s distance.geodesic method and the Haversine formula and the measured distance is 38m. The distance calculated with the Bokeh ScaleBar is 57m.

The error might be that the longitude and the latitude are switched when computing the scale value in the Bokeh method (as I found the same distance with the Geopy method when I made that mistake).

I have tried to change the orientation, specify the fig.x_range or fig.y_range, put the fixed length for the bar but it was still incorrect.

Here are the results with other tools:

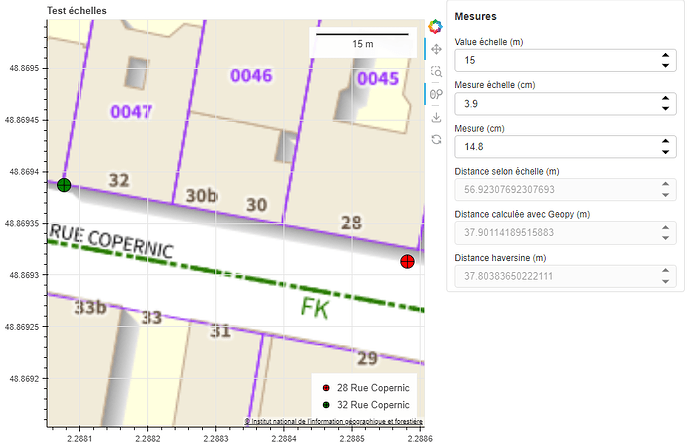
Here is the result of the example above:

Is this a bug or is there a parameter I could use to fix this?

Jonas_Grave_Kristens · December 17, 2024, 1:34pm

@ernhollam I use a CustomJS function in order to have the Scalebar show correct distance when using map data. I calculate distance using the haversine formula.
When defining the ScaleBar you need to specify a custom range that covers the x-axis (if horizontal scalebar).

scale_bar = ScaleBar(
        range = Range1d(start=0, end=1000),
        bar_length = 120,
        bar_length_units = 'screen',
        location = 'top_right',
        name = 'scale_bar'
        )

In the CustomJS function I calculate the distance based on a diagonal in the middle of the plot canvas and then translate that to a value that the range covers (x-axis). I am not good on the internals of BokehJS so my code might be inefficient.

map_ruler_js = '''
    function canvasLatLonMid(frame, px_len) {
        const xscale = frame.x_scale;
        const yscale = frame.y_scale;
        const {x0, y0, x1, y1} = frame.bbox;

        const half_dist = Math.sqrt( ((px_len/2)**2) / 2 );
        const x0_dia = (x0+x1)*0.5 - half_dist;
        const x1_dia = x0_dia + 2*half_dist;
        
        const y0_dia = (y0+y1)*0.5 - half_dist;
        const y1_dia = y0_dia + 2*half_dist;

        const p1 = projections.wgs84_mercator.invert(xscale.invert(x0_dia), yscale.invert(y0_dia));
        const p2 = projections.wgs84_mercator.invert(xscale.invert(x1_dia), yscale.invert(y1_dia));
        
        return {p1, p2};
    }

    function greatCirleDistance(point1, point2) {
        /* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -  */
        /* Latitude/longitude spherical geodesy tools                         (c) Chris Veness 2002-2021  */
        /*                                                                                   MIT Licence  */
        /* www.movable-type.co.uk/scripts/latlong.html                                                    */
        /* www.movable-type.co.uk/scripts/geodesy-library.html#latlon-spherical                           */
        /* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -  */
        // Calculate great-circle distance between two points based on haversine formula (ref above).
        // point data format: [lon, lat]

        const lon1 = point1[0]
        const lat1 = point1[1]
        const lon2 = point2[0]
        const lat2 = point2[1]
        
        const R = 6371e3 // metres
        const φ1 = lat1 * Math.PI/180 // φ, λ in radians
        const φ2 = lat2 * Math.PI/180
        const Δφ = (lat2-lat1) * Math.PI/180
        const Δλ = (lon2-lon1) * Math.PI/180

        const a = Math.sin(Δφ/2) * Math.sin(Δφ/2) +
                Math.cos(φ1) * Math.cos(φ2) *
                Math.sin(Δλ/2) * Math.sin(Δλ/2)
        const c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1-a))

        return R * c; // in metres
    }
    const projections = Bokeh.require("core/util/projections");
    const p_obj = Bokeh.index[Object.keys(Bokeh.index)[0]];
    const scale_bar = p.select(name = 'scale_bar')[0];
    const ruler_px_len = scale_bar.bar_length;
    
    const rng_span_px = scale_bar.orientation == "horizontal" ? p_obj.frame.bbox.width : p_obj.frame.bbox.height;

    const {p1, p2} = canvasLatLonMid(p_obj.frame, ruler_px_len);
    let dist = greatCirleDistance(p1, p2);
    console.log(dist);
    // if you want to plot the points used for the diagonal
    const p1_m = projections.wgs84_mercator.compute(p1[0], p1[1]);
    const p2_m = projections.wgs84_mercator.compute(p2[0], p2[1]);
    console.log(p1_m);
    console.log(p2_m);
    
    src['points'].data = {
        'x': [p1_m[0], p2_m[0]],
        'y': [p1_m[1], p2_m[1]]
    }

    scale_bar.range.end = dist/ruler_px_len * rng_span_px;
'''

Need to call the CustomJS on initial document layout, and subsequently when any updates on the canvas with respect to zoom, panning, etc.

# src for points for diagonal if one wants to plot those
src = ColumnDataSource(data = {'x': [], 'y': []})

callback = CustomJS(
    args = {
        'p': p_map,
        'xaxis': p_map.xaxis,
        'src': src 
    },
    code = map_ruler_js
)
curdoc().js_on_event("document_ready", callback)

p_map.js_on_event('lodstart', callback)
p_map.js_on_event('lodend', callback)
p_map.js_on_event('pan', callback)
p_map.js_on_event('wheel', callback)

gmerritt123 · December 17, 2024, 2:00pm

I have implemented basically the same thing for my geologic cross section applications. User draws lines on a epsg:3857 map, but the cross section coordinates need to be distance and metres above sea level for x-y respectively, so I have to a) segment the line they drew to a resolution higher than the geologic model’s raster resolution (model is just a stack of elevation rasters for each model layer), b) Project the nearest raster cell values to the line segments, and (finally the relevant part) c) convert the map xy coordinates of each line segment to a cumulative distance along the line, which relies on haversine:

You’ll see I’m also using CustomJSTicker to convert the x-axis ticks on plan view to “be the scalebar” as well, which does a similar action to what you outlined.

Just wanted to chime in/share since it’s a funny case of convergent evolution

Bryan · December 17, 2024, 3:17pm

Is there a change or improvement to make here on the bokeh side?

gmerritt123 · December 17, 2024, 3:40pm

I guess the main concern/question would be IF the relatively new (i.e. I haven’t even used it yet, still relying on my custom stuff above) Scalebar is able to recognize a mercator range and do the haversine calculation correctly. I don’t know but it seems OP is saying no.

ernhollam · December 17, 2024, 3:41pm

Hi,

Yes, the length (=value) of the ScaleBar is not correct, it gives greater distances than it really is.

I don’t have access to the code that does the caculation of the value of the scale when using the ScaleBar annotation but there might be a bug.

The geopy method takes pair of (lat, lon) tuples and I initially put (lon, lat) tuple instead and found the same incorrect distance as the one given by the Bokeh ScaleBar.

Bryan · December 17, 2024, 3:42pm

I definitely don’t know the details in this case but it seems as though a GitHub Issue would be reasonable.

ernhollam · December 17, 2024, 4:32pm

Link to GitHub issue is here